密码学
这个文档里面大部分内容都是来自网络,平常自学的简单整理,密码学很深奥,我还属于门外汉,如果有任何错误请联系我进行修改
链接:
- 比特币研究室:https://panzhibiao.com/
- 密码学:https://zxy110.github.io/zxy/2019/03/26/%E5%AF%86%E7%A0%81%E5%AD%A6/
- 登链社区-区块链中的数学:https://learnblockchain.cn/tags/%E5%8C%BA%E5%9D%97%E9%93%BE%E4%B8%AD%E7%9A%84%E6%95%B0%E5%AD%A6
- 常用的算法:https://docs.github.com/cn/authentication/managing-commit-signature-verification/generating-a-new-gpg-key
- 密码学系统:https://www.jianshu.com/p/e40f4f7838a8
DH:Diffie-Hellman 密钥交换的原理
交换双方可以在不共享任何秘密的情况下协商出一个密钥。
- Diffie-Hellman 交换过程中涉及到的所有参与者定义一个组,在这个组中定义一个大质数 p,底数 g。
- Diffie-Hellman 密钥交换是一个两部分的过程,Alice 和 Bob 都需要一个私有的数字 a,b。
下面是 DH 交换的过程图:
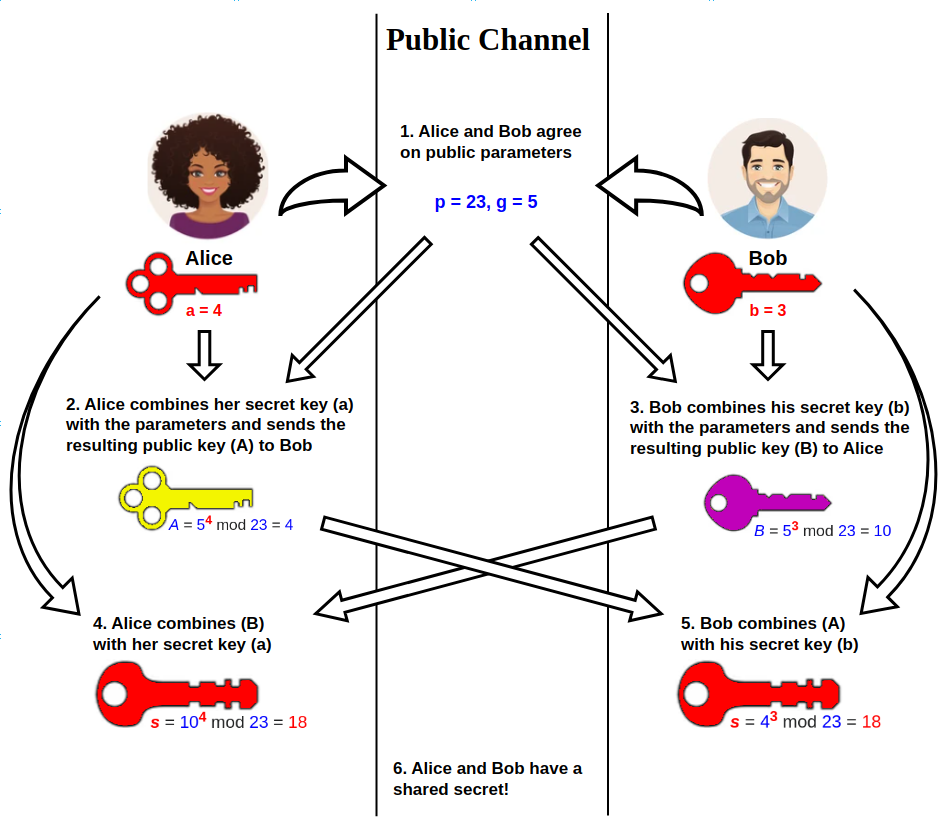
下面我们进行一个实例
- 爱丽丝与鲍伯协定使用 p=23 以及 g=5.
- 爱丽丝选择一个秘密整数 a=6, 计算 A = g^a mod p 并发送给鲍伯。 A = 5^6 mod 23 = 8.
- 鲍伯选择一个秘密整数 b=15, 计算 B = g^b mod p 并发送给爱丽丝。 B = 5^15 mod 23 = 19.
- 爱丽丝计算 s = B^a mod p 19^6 mod 23 = 2.
- 鲍伯计算 s = A^b mod p 8^15 mod 23 = 2.
- 他们的公共秘钥就是 2
RSA
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。RSA是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在1977年一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA加密算法是一种非对称加密算法,对极大整数做因数分解的难度决定了 RSA 算法的可靠性。
换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的 RSA 钥匙才可能被强力方式破解。到2020年为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被破解的。
假设爱丽丝想要通过一个不可靠的媒体接收鲍伯的一条私人信息。她可以用以下的方式来产生一个公钥和一个私钥:
随意选择两个大的素数p和q,p不等于q,计算N=pq。
根据欧拉函数,求得\({\displaystyle r=\varphi (N)=\varphi (p)\times \varphi (q)=(p-1)(q-1)}{\displaystyle r=\varphi (N)=\varphi (p)\times \varphi (q)=(p-1)(q-1)}\)
选择一个小于r的整数e,使e与r互质。并求得e关于r的模逆元,命名为d(求d令\({\displaystyle ed\equiv 1{\pmod {r}}}{\displaystyle ed\equiv 1{\pmod {r}}}\))。(模逆元存在,当且仅当e与r互质)
将p和q的记录销毁。
(N,e)是公钥,(N,d)是私钥。爱丽丝将她的公钥(N,e)传给鲍伯,而将她的私钥(N,d)藏起来。
像Arweave就在使用:https://github.com/ArweaveTeam/arweave-js
算法:https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95
ECC
椭圆曲线加密(Elliptic Curve Cryptography)算法。
公开密钥算法总是要基于一个数学上的难题。比如 RSA 依据的是:给定两个素数 p、q 很容易相乘得到 n,而对 n 进行因式分解却相对困难。那椭圆曲线上有什么难题呢?
考虑如下等式:
K=kG [其中 K,G 为 Ep(a,b)上的点,k 为小于 n(n 是点 G 的阶)的整数]
不难发现,给定 k 和 G,根据加法法则,计算 K 很容易;但给定 K 和 G,求 k 就相对困难了。
加密通信的过程:
- 用户 A 选定一条椭圆曲线 Ep(a,b),并取椭圆曲线上一点,作为基点 G。
- 用户 A 选择一个私有密钥 k,并生成公开密钥 K=kG。
- 用户 A 将 Ep(a,b)和点 K,G 传给用户 B。
- 用户 B 接到信息后 ,将待传输的明文编码到 Ep(a,b)上一点 M(编码方法很多,这里不作讨论),并产生一个随机整数 r(r
- 用户 B 计算点 C1=M+rK;C2=rG。
- 用户 B 将 C1、C2 传给用户 A。
- 用户 A 接到信息后,计算 C1-kC2,结果就是点 M。因为 C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M
再对点 M 进行解码就可以得到明文。
椭圆曲线加密算法:https://www.jianshu.com/p/e41bc1eb1d81
ECDH 密钥交换
ECC 算法和 DH 结合使用,用于密钥磋商,这个密钥交换算法称为 ECDH。
ECC 是建立在基于椭圆曲线的离散对数问题上的密码体制,给定椭圆曲线上的一个点 P,一个整数 k,求解 Q=kP 很容易;给定一个点 P、Q,知道 Q=kP,求整数 k 却是一个难题。
ECDH 即建立在此数学难题之上。密钥磋商过程:
假设密钥交换双方为 Alice、Bob,其有共享曲线参数(椭圆曲线 E、阶 N、基点 G)。
- Alice 生成随机整数 a,计算 A=a*G。 #生成 Alice 公钥
- Bob 生成随机整数 b,计算 B=b*G。 #生产 Bob 公钥
- Alice 将 A 传递给 Bob。A 的传递可以公开,即攻击者可以获取 A。由于椭圆曲线的离散对数问题是难题,所以攻击者不可以通过 A、G 计算出 a。
- Bob 将 B 传递给 Alice。同理,B 的传递可以公开。
- Bob 收到 Alice 传递的 A,计算 Q =b*A #Bob 通过自己的私钥和 Alice 的公钥得到对称密钥 Q
- Alice 收到 Bob 传递的 B,计算 Q`=a*B #Alice 通过自己的私钥和 Bob 的公钥得到对称密钥 Q’
Alice、Bob 双方即得 \(Q=b*A=b*(a*G)=(b*a)G=(a*b)*G=a(b*G)=a*B=Q’\) (交换律和结合律),即双方得到一致的密钥 Q。
通信双方(Alice 和 Bob)需要安全的交换信息,但是通信过程中第三方可能会拦截并窃听,但是要求第三方不能解密这些加密信息。这也是 TLS 使用的原则之一。
ECDSA
ECDSA 的全名是 Elliptic Curve DSA,即椭圆曲线 DSA。它是 Digital Signature Algorithm (DSA)应用了椭圆曲线加密算法的变种。
椭圆曲线算法的原理很复杂,但是具有很好的公开密钥算法特性,通过公钥无法逆向获得私钥。
-a 加法逆元: a + (-a) = 0
a^-1 乘法逆元: a * (a^-1) = 1
ECDSA 算法主要包括以下四个关键功能:
产生密钥 GenKey
- 选择一条椭圆曲线 E_P(a,b),选择基点 G,G 的阶数为 n
- 选择随机数 d ∈n 为私钥,计算公钥 Q = d⋅G
签名算法 Sign
- 对消息 m 使用消息摘要算法,得到 z=hash(m)
- 生成随机数 k∈n,计算点(x, y)=k⋅G
- 取 r=x mod n,若 r=0 则重新选择随机数 k
- 计算 s = k^−1(z+rd) mod n,若 s=0 则重新选择随机数 k
- 上述(r,s)即为 ECDSA 签名
验证算法 Verify
使用公钥 Q 和消息 m,对签名(r,s)进行验证。
- 验证 r,s∈n
- 计算 z = hash(m)
- 计算 u_1 =zs^−1 mod n 和 u_2 = rs^−1 mod n
- 计算(x, y) = u1⋅G+u2⋅Q mod n
- 判断 r == x,若相等则签名验证成功
恢复算法 Recover
已知消息 m 和签名(r,s),恢复计算出公钥 Q。
- 验证 r, s∈n
- 计算 R=(x, y),其中 x=r,r+n,r+2n…,代入椭圆曲线方程计算获得 R
- 计算 z = hash(m)
- 计算 u1 = −zr^−1 mod n 和 u2 = sr^−1 mod n
- 计算公钥 Q= (x’, y’)=u1⋅G+u2⋅R
椭圆曲线的参数可以有多种配置方式,也就存在多种不同的曲线,例如secp256k1、secp256r1等,不同曲线的安全性存在一些区别
Schnorr 签名
Schnorr 签名算法几乎在各个层面均优于比特币现有的签名算法 ECDSA:性能,安全,体积,扩展性等方面。
Schnorr Sig 可以与 ECDSA 使用同一个椭圆曲线:secp256k1 curve,升级起来的改动非常小。
原理
我们定义几个变量(大写为点或函数,小写为数字):
- G:椭圆曲线。
- m:待签名的数据,通常是一个 32 字节的哈希值。
- x:私钥。P = xG,P 为 x 对应的公钥。
- H():哈希函数。 . 示例:写法 H(m || R || P)可理解为:将 m, R, P 三个字段拼接在一起然后再做哈希运算。
生成签名
签名者已知的是:G-椭圆曲线, H()-哈希函数,m-待签名消息, x-私钥。
- 选择一个随机数 k, 令 R = kG
- 令 s = k + H(m || R || P)*x
那么,公钥 P 对消息 m 的签名就是:(R, s),这一对值即为 Schnorr 签名。
注:一种 k 的生成方式:k=H(m||x),能够保证同一个消息的签名结果永远一致,避免钓鱼签名。
上面的 H()的参数添加了 R,所以能够保证 H()的结果永远是改变的,也无法钓鱼签名。
验证签名
验证者已知的是:G-椭圆曲线, H()-哈希函数,m-待签名消息, P-公钥,(R, s)-Schnorr 签名。验证如下等式:
sG = R + H(m || R || P)P
若等式成立,则可证明签名合法。
我们推演一下,此过程包含了一个极其重要的理论:椭圆曲线无法进行除法运算。
- s 值的定义:s = k + H(m || R || P)*x,等式两边都乘以椭圆曲线 G,则有:
- sG = kG + H(m || R || P)*x*G,又因 R = kG, P = xG,则有:
- sG = R + H(m || R || P)P,椭圆曲线无法进行除法运算,所以第 3 步的等式,无法向前反推出第 1 步,就不会暴露 k 值以及 x 私钥。同时,也完成了等式验证。
组签, Group Signature(多签)
一组公钥,N 把,签名后得到 N 个签名。这个 N 个签名是可以相加的,最终得到一个签名。这个签名的验证通过,则代表 N 把公钥的签名全部验证通过。
有:
- 椭圆曲线:G
- 待签名的数据:m
- 哈希函数:H()
- 私钥:x1,x2,公钥:P1=x1G, P2=x2G
- 随机数:k1, k2,并有 R1=k1G, R2=k2G
- 组公钥:P = P1 + P2
则有:
- 私钥 x1 和 x2 的签名为:(R1, s1), (R2, s2)。
- 两个签名相加得到组签名:(R, s)。其中:R = R1 + R2, s = s1 + s2。
推演过程:
- 令 R = R1 + R2, s = s1 + s2
- 已知:s1 = k1 + H(m || R || P)*x1,s2 = k2 + H(m || R || P)*x2
- s = s1 + s2 = k1 + H(m || R || P)*x1 + k2 + H(m || R || P)*x2 = (k1 + k2) + H(m || R || P)(x1 + x2)
- 两边同时乘以 G,则有: sG = (k1 + k2)G + H(m || R || P)(x1 + x2)G = (k1G + k2G) + H(m || R || P)(x1G + x2G) = (R1 + R2) + H(m || R || P)(P1 + P2) = R + H(m || R || P)P
- 完成证明,并从两个合作方推演至 N 个合作方
组公钥(Group Key),是 N 把公钥进行相加后的值,又称聚合公钥(Aggregation Key)。
需要指出的是,参与方需要先相互交换公钥和 R 值,然后再进行各自的签名。
Schnorr 签名介绍:https://panzhibiao.com/2019/02/28/schnorr-sigature/ eth 合约的实现:https://github.com/HarryR/solcrypto/blob/master/contracts/Schnorr.sol
EdDSA
Ed25519是基于Edwards曲线的数字签名算法(EdDSA),结合 SHA-512/256哈希算法,采用扭曲爱德华曲线。
签名过程不依赖随机数生成器,不依赖hash函数的防碰撞性,没有时间通道攻击的问题,并且签名很小,只有64字节,公钥也很小,只有32字节。
安全性高,一个椭圆曲线加密算法就算在数学上是安全的,在实用上也并不一定安全,有很大的概率通过缓存、时间、恶意输入摧毁安全性,而 25519 系列曲线经过特别设计,尽可能的将出错的概率降到了最低,可以说是实践上最安全的加密算法。
https://learnblockchain.cn/article/1663
密码学安全性对比:https://safecurves.cr.yp.to/index.html
零知识证明
最简单的零知识证明:a*G+b*G = (a+b)*G,用户不需要提供 a 和 b,而是提供 aG 和 bG
同态加法:加密后相加 = 相加后加密 (椭圆曲线)
同态乘法:加密后相乘 = 相乘后加密 (RSA)
全同态加密(Gentry同态加密)
PLONK 电路原理:https://zhuanlan.zhihu.com/p/343211926,被用于 zkSync
什么是 zkSNARKs:https://ethfans.org/posts/what-is-zksnarks-spooky-moon-math-part-1
zk-stark:https://www.chainnews.com/articles/621681266821.htm
ZK-Rollup 开发经验分享:https://www.fluidex.io/zh/blog/zkrollup-intro1/
零知识证明的通俗易懂的故事解释:https://its401.com/article/zjg555543/89333948
STARKs, Part I: 多项式证明:https://www.jianshu.com/p/ffb6b475312a
何谓零知识证明?:https://learnblockchain.cn/article/2445
用途
零知识证明常用于以下场景:
- 证明隐私数据情况:
- 一个人的银行账户金额多于 X;
- 去年,一家银行未与实体 Y 进行交易;
- 一个人的信用评分高于 Z;
- 在不暴露全部 DNA 数据的前提下匹配 DNA
- 匿名认证:
- 在不揭露身份的情况下(比如登录密码),证明请求者R有权访问网站的受限区域;
- 证明一个人来自一组被允许的国家/地区列表中的某个国家/地区,但不暴露具体是哪个;
- 证明一个人是某机构会员但不是是谁。
- 匿名支付/代币:
- 区块链中的(不可追踪的)隐私币; 付款完全脱离任何一种显示身份;
- 纳税而不透露收入;
- 外包计算
- 将昂贵的计算任务外包,并在不重新执行的情况下验证计算结果是否正确;它打开了一种零信任计算的类别;
- 改进区块链模型,从所有节点做同样的计算,到只需一方计算然后其它节点进行验证1. 等,zk rollup layer2方案等。
SSS(Shamir’s Secret Sharing)
Shamir 秘密分享需要复原主私钥,而不是像多重签名或者门限签名, 主私钥从来没有重建过,哪怕是在内存或者缓存中,对于至关重要的账户而言,这种短暂的重建也是不能容忍的。
基于一元n次方程y=f(x),如果有n个不同的值(x,y),就能够算出方程的系数,从而得到函数f(x),其中f(0)就是秘密。
\[f(x) = s + a_1x + a_2x^2 + a_3x^3 + ... + a_{n-1}x^{n-1} \bmod p\]有限域(finite field)
- 也叫伽罗瓦域(Galois field):https://zh.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E5%9F%9F
- 模逆元:https://zh.wikipedia.org/wiki/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
- 有限域算术:https://zh.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E5%9F%9F%E7%AE%97%E6%9C%AF
门限签名机制(Threshold Signature Schemes)
门限密钥生成(Thresh-Key-Gen):基于安全参数构造一种分布式密钥生成协议 DKG,协议运行输出一个共同的公钥 pk 和分属不同参与方各自所有的私钥份额 ski,聚集起满足阈值数量的私钥份额可以构建出真正的私钥 sk。
门限签名(Thresh-Sig):基于分布式通信网络,各参与方通过自己的私钥份额 ski 完成对消息 m 的分布式协作签署并输出最终的可验证签名 Sig(sk, m),这个签名跟单独用 sk 私钥签出的一模一样,可以用所基于的基础签名机制里的验证函数进行本地验证,无需走通信交互验证
BLS
BLS(Boneh–Lynn–Shacham): 该方案验证效率尚可,但在签名聚合环节,生成签名的耗时会随参与者数量的增加而显著增加,可以达到毫秒级,比传统的数字签名方案慢几个数量级。
目前的门限签名方案在初始化过程中,如果不依赖可信第三方,会面临交互轮数过多、构造复杂等问题。以上工程问题对需要进行高频签名操作的应用来说,可能会带来一定性能上的挑战,但对于一般应用来讲,应该不会成为性能瓶颈。
https://gist.github.com/hermanjunge/3308fbd3627033fc8d8ca0dd50809844
https://www.cryptologie.net/article/472/what-is-the-bls-signature-scheme/
多方计算
TEE
TEE(Trusted Execution Environment)可信执行环境
常规操作系统REE(Rich Execution Environment)
可信执行环境技术简介:https://segmentfault.com/a/1190000037622124
技术介绍:https://blog.csdn.net/trustbo/article/details/78234373
定义及实现形态:https://www.secrss.com/articles/13922
不经意传输(Oblivious Transfer)
来看一个例子:假设某旅行社拥有 N 个景点的旅游资料,小淘想去其中的 A 景点游玩,希望向旅行社购买相关资料做好出游功课。但是小淘非常在意自己的隐私,不希望向旅行社泄露自己的目的地是哪里。因此双方希望这笔交易能够满足以下隐私条件:
- 小淘不希望向旅行社泄露“我准备去 A 景点”这一信息;
- 旅行社只希望出售小淘出钱购买的那份资料,而不泄露小淘未购买的 N-1 份资料;
粗看起来这种隐私条件似乎是无法满足的:旅行社只要把景点 A 的资料给到小淘,就必然了解了“小淘正在关注 A 景点”这一信息;除非旅行社把所有 N 份资料都给出,但是这又违背了旅行社的利益;
但是神奇的 OT 可以让交易在这种“不可能的条件”下达成。简而言之,在 OT 协议中,旅行社把他拥有的 N 份资料使用某种双方协商同意的加密算法和参数进行加密,然后发送给小淘;小淘可以从密文中解密出 A 的资料,而无法解密出其他 N-1 份资料。

混淆电路
任意函数最后在计算机语言内部都是由加法器、乘法器、移位器、选择器等电路表示,而这些电路最后都可以仅由 AND 和 XOR 两种逻辑门组成。一个门电路其实就是一个真值表,例如 AND 门的真值表就是:
| and | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
https://www.jinse.com/news/blockchain/841523.html
https://www.8btc.com/media/650794
https://www.163.com/dy/article/FL563MAE0519SM7A.html
pgp
- 链接
- 功能:加密、签名、认证
- 可以创建 subKeys,使用 subKeys 进行操作,避免 Master key 泄露
- master key 可以授权、撤销 subKeys,依赖于公钥服务器(授权信息都放在公钥服务器)
门罗
VDF&VRF
VRF
可验证随机数 https://blog.chain.link/chainlink-vrf-on-chain-verifiable-randomness-zh/
VDF
可验证延迟函数 https://github.com/keyfuse/vdf